12年前的作品──《美绿中国象棋》制作过程及算法简介
这个游戏是大学本科二年级时(1998年)修人工智能课程的功课 。这个游戏的「棋力」并不高,主要是因为没有花时间在调整的工作上。比较满意的部分是使用 OpenGL 做的使用者介面。本文将简单介绍制作本游戏的过程及当中用到的算法。
你可以先下载(1049KiB)试试,但现时已找不到源码了,将来找到的话再分享。
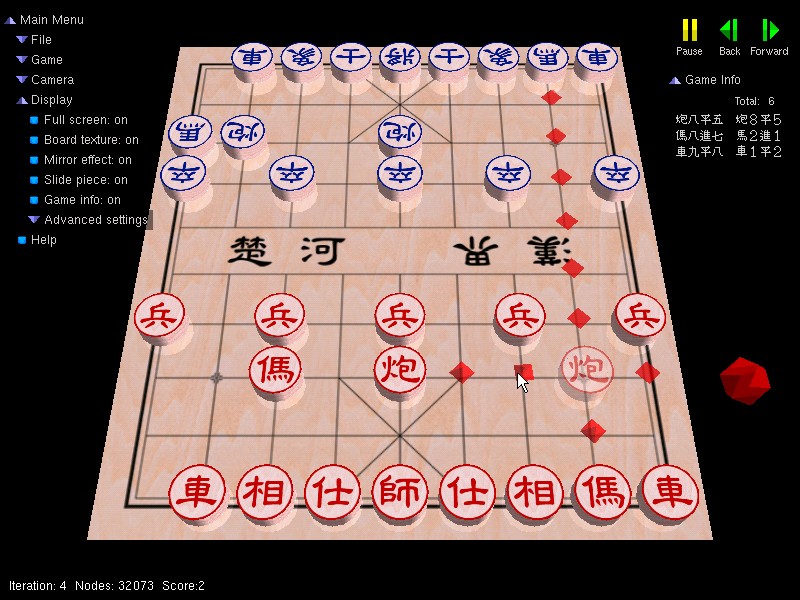
制作过程
约在接到这项功课前的一个月,刚开始自学 OpenGL,因此便考虑利用 OpenGL 做使用者接口。
以前写程式都是会先写使用者接口,用来显示程式的一些资料,之后再写算法,游游戏也不例外。我利用 Photoshop 及 Illustrator 绘制棋子及棋盘,再尝试写程序(Visual C++ 6.0)以立体方式显示它们。由于太想试一试 OpenGL 的能力,在制作初期已加上了棋盘反射的效果。
之后便建构程序的重要资料结构,为每种棋子设定可行走法,有些棋子是颇麻烦的,例如炮除了可四方向移动外,还能隔子吃棋。做好了这些规则,便加入使用者介面的输入部分,可以进行人对人的游戏。
至于人工智能部分,首先写最简单的搜寻演算法──极大极小搜索(minimax search)。最初使用的评估函数(evaluation function)只是双方余下棋子的数目的差,那么电脑会避免自己的棋子被吃,又会尽量去吃对方的棋子,可谓已有一点「智能」了。 然后着手改良搜寻方法,使搜寻的速度提高。与此同时,参考了吴身润先生的作品,去编写评估函数。之后更加入了二千个棋谱走法 (book moves)。
接着得到各方好友的帮助,替它进行测试,以改善评估函数。我同时制作其余的使用者接口部分,包括左上方的选单、右方的按钮及棋局资料显示。
整个制作过程历时两个月,幸好在功课期限前的一个星期是假期,能通宵达旦去完成。
算法简介
这里简介这游戏中用到的人工智能相关的算法。
游戏树
如同大部份中国象棋程序,这游戏也是从游戏树(game tree)中找出最好的走法(move)。
在游戏树中,每个节点代表游戏的一个状态(state),而每条边是一个合法的走法。因为象棋是双方轮交替下棋(红 → 黑 → 红 → …),所以树中每对相邻的层阶都是双方各自可走的走法。下图(來源)显示了打井游戏的部份游戏树。
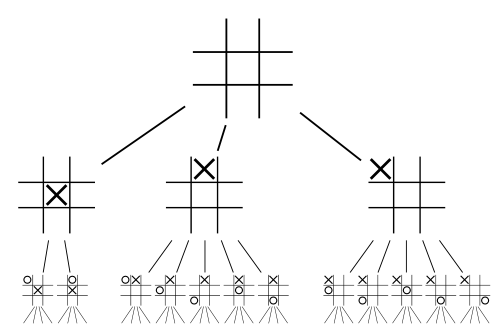
在打井游戏中,由于最多是 9 步,它的游戏树深度为 9,每一步之后,合法的走法变少了一个。因此,这个游戏树的总节点数目为 1 + 9 + 9 × 8 + 9 × 8 × 7 + … = 986410。假设有了这个游戏树,我们只要从树中找出目前状态的节点,再往下搜索到任何一个获胜的叶节点(我方胜利终局),从当前节点走到该叶节点就是「必胜之道」,所以只要按「必胜之道」的第一步去走就会胜利了。事实上,写一个不会输的打井游戏搜索 AI 只需要十数行代码左右。
最小最大搜索
不过,中国象棋的游戏树是非常大的(虽然比围棋小),不可把整个树储存或搜索至叶节点(终局除外)。因此,只能搜到某个深度,并在该深度的节点进行启发评估 (heuristic rvaluation),这估值反映了该节点棋局对我方的优势。
由于在我方下棋的层数,我们会在每个节点选择子节点中最大评估值,作为本节点的评估值;在对方的层数,我们会假设他选择最小启评估值的节点;这就是最小最大搜索(minimax search)的原理。
为了简化程序,不用按层数选择用 min 或 max,minimax 通常在实现的时候会采用 negamax 方式。其原理就是每层都是取下一层结果的负值的最大值。
所有 Minimax 搜索都可以做到安全的上下界剪枝,称为 alpha-beta 剪枝(alpha-beta bruning),这里不详述了。
以下是这游戏中用到的方式:
AlphaBeta(alpha, beta, depth) {
if (depth == 0)
return Quiescence(alpha, beta);
succ = generate all move from current board
sort succ by estimate function
for each node n in succ {
makeMove(n);
x = -AlphaBeta(alpha, beta, depth - 1);
takeBack();
if (x > alpha) {
if (x >= beta)
return beta;
alpha = x;
// update principal variation here
}
}
if (no legal move)
return -10000 + ply;
return alpha;
}
平静搜索
当搜索到最大深度的时候,有机会在下一步会产生很大的评估值变化(例如被吃子)。平静搜索(quiescence search)就是在最大深度的时候继续搜索,直至局势变得稳定。
迭代深化
在 alpha-beta 剪枝中,如果能尽快缩小上下界,将会减少搜索的节点数目。这就产生了迭代深化(iterative deepening) 的优化方法。相对于直接搜索深度为N的树,先搜索深度为i,并用其结果来优化深度为 i + 1 的搜索。
所谓结果,是指在 alpha-beta 剪枝发生时去记录principal variation,并利用这个来排序下迭代里产生的走法。
游戏树中会有很多相同的节点。为免重覆计算节点,这游戏也使用了transposition table技术。
走法产生
在搜索中,产生合法走法占很大的时间。因此,游戏状态的表示方式和走法产生是非常重要的。而产生的走法也用在用户界面上:
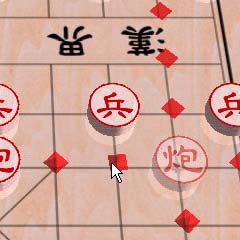
因为没有源代码,我记忆中,这游戏同时采用了「棋子→位置」及「位置→棋子」两个数组去表达棋盘的状态。例如车的移动要向四个方向产生走法,就可以用「位置→棋子」的数组去检查某位置是否有其他棋子。
在开局时,会首先寻找开局库有没有记录,这时候会用到一个更紧凑的棋盘表达方法。
评估方式
一个象棋的「智能」就在于其评估棋局的能力,上面提到的各种搜索优化只是用来加速搜寻(但在同等时限里增加搜索的节点也能增加「棋力」)。评估方法花费的时间也大大影响整体速度,所以必须平衡评估函数的能力及花费时间。
这个游戏采用的静态评估分数为(在结合其他评估时,把这值乘以系数 10):
- 士 6
- 象 6
- 马 13
- 车 52
- 炮 22
- 兵 2
如前文提及,只是按棋盘余下的棋子,按这个分数来计算评估值,已可以有不少的「棋力」。这么简单的评估已令到计算机懂得「将军抽车」,我这个象棋门外汉会输给深度4的搜索。
我按照 [1],加入了单独棋子位置的分数,及一些全局分析的分数,例如:
- 车迟开步 -13
- 车在马后 -8
- 炮在马后 +8
- 马路被封 -4
要获得更好的评估方式,可以靠人的经验、分析专业棋谱、人工智能自动学习等等方法。
回顾感想
这个程式是我比较喜欢的作品,从外表(使用者接口)到内函(人工智能)都颇满意。而在开发过程中也真正地学会了课堂和课本的知识。
在开发这个游戏中,我也学习了象棋的一些规则,例如胜利条件不是吃了对方的将军,而是对手没步可走。但平手的规则并没有完成。
没想到十二年后,这个程序依然可以在 Windows 7 上运行自如(NT/2000/XP/Vista 也沒問題),这要赞一下微软。外表上,大概是用了比较简单而独特一点的设计,包括渲染和 GUI 等也不会感到很落后。不过,当年应该没有使用系统时钟,使现在棋子移动得太快,这算是一个缺憾吧。
在进入社会工作以后,我很少有机会自己一个人写程序,编程的热情也不如当天。但我会继续在家里编程,希望能回复一点当日的热血。
参考
[1] 吴身润, 人工智慧程式设计:象棋, 旗标出版股份有限公司, 1996. [2] George F. Luger, William A. Stubblefield, Artificial Intelligence: Structures and Strategies for Complex Problem Solving 2nd Edition, The Benjamin/Cummings Publishing Co. Inc., 1992.
Milo Yip
MISC
